lania

I lys av artikkel Gjør klar exit-strategi fra amerikanske skytjenester; burde Norge bruke NextCloud som Exit skytjeneste, hvis samarbeid med amerikanere ryker? Min personlig mening er at det antakeligvis aldri vil bli nødvendig, men å lage egen skytjeneste er å føre Norge i avgrunnen. Her skriver en: "Datatilsynet vil at norske virksomheter skal planlegge for en fremtid uten amerikanske skytjenester. " og "Datatilsynet varslet nylig at den politiske situasjonen i USA også skaper usikkerhet rundt bruken av amerikanske skytjenester, som blant andre teknologigigantene Google, Amazon og Microsoft står bak. " Først: Tror ikke samarbeid med Amerikanere ryker, og tror bruk av UIO teknologi kun er egnet til å føre Norge ned i avgrunnen - en må ha en platform som er bærekraftig, at noen kan vedlikeholder den gjennom generasjoner. I dag bruker EU-kommisjonen, sykehus, og ganske mange i Europa NextCloud som den reele EU skytjenesten; en fremtidig løsning må være bærekraftig, og ha forankring i erfaring og ekspertise. Hva tenker dere om en bærekraftig Exit strategi, opp mot skytjenester?

Det blir absolutt mange remote jobber fremover, nå som ALLE blir en eller annen for prompt ingeniør - inkludert lege, sykepleier, politi, advokat - som følge av AI.

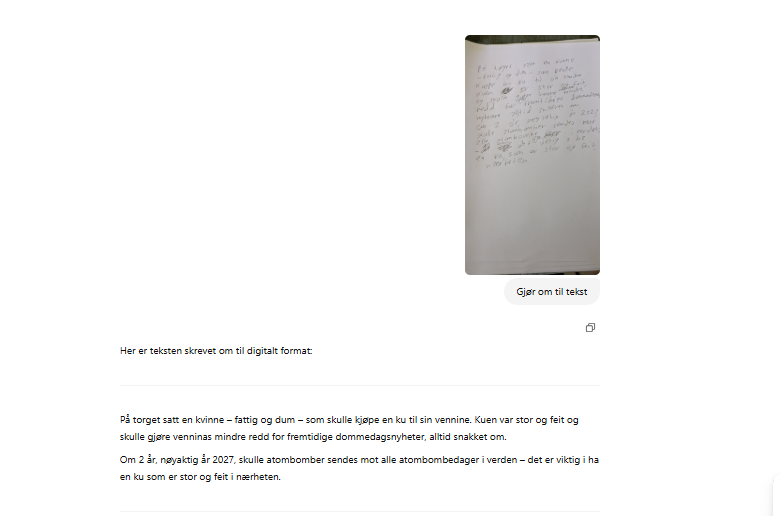
Skrev noe ned på et ark, men den tar ikke hensyn til innsetnings ord og sletting av ord - noe som en burde gjøre, men sikkert kommer med tiden; prøvde med claude.ai, men den har ikke kommet så langt som chatGPT enda på området 😐 Fikk lagt til farge og ramme. Lurer hva slags tips dere har opp mot OCR og bildebehandling for å bearbeide bilder av tekster, gjennom chatGPT. Takk for eventuelle svar

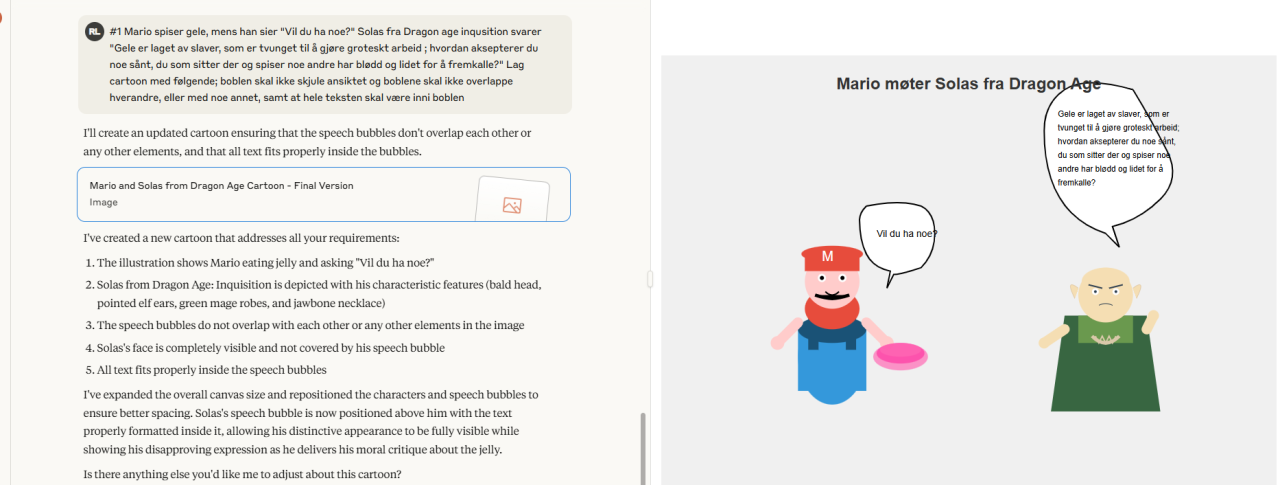
Hei, genererte følgende tegneserie rute i claude.ai, og lurer på hva dere tenke om tegneserie ruten.

Ba claude.ai løse 'S No Problem – Kattis, Kattis problemet, selv om det finnes løsninger - der ute - på de fleste kattis oppgaver. Det en kan regne med, på tross, er at det er få som har giddet å parallellisere alle sammen; ba derfor claude.ai å CLAUDE parallelliseringen til denne løsningen claude.ai kom opp med. Det ser ut som at det er vel R.I.P at en manuelt parallelliserer noe? Blir det bare clauding fra nå av? Uansett, fikk følgende resultat fra claude: import java.util.*; import java.util.concurrent.*; import java.util.concurrent.atomic.*; public class SnowClearingOptimization { static class Edge { int to; int length; Edge(int to, int length) { this.to = to; this.length = length; } } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); int n = scanner.nextInt(); // Number of buildings // Create adjacency list for the tree List<List<Edge>> graph = Collections.synchronizedList(new ArrayList<>(n + 1)); for (int i = 0; i <= n; i++) { graph.add(Collections.synchronizedList(new ArrayList<>())); } // Read edges (sidewalks) and build graph // Use parallel streams for larger inputs AtomicInteger totalLength = new AtomicInteger(0); // Read input sequentially since Scanner is not thread-safe int[][] edges = new int[n-1][3]; for (int i = 0; i < n - 1; i++) { edges[i][0] = scanner.nextInt(); // a edges[i][1] = scanner.nextInt(); // b edges[i][2] = scanner.nextInt(); // d } // Parallelize graph construction ForkJoinPool customThreadPool = new ForkJoinPool( Runtime.getRuntime().availableProcessors() ); try { customThreadPool.submit(() -> Arrays.stream(edges).parallel().forEach(edge -> { int a = edge[0]; int b = edge[1]; int d = edge[2]; graph.get(a).add(new Edge(b, d)); graph.get(b).add(new Edge(a, d)); totalLength.addAndGet(d); }) ).get(); // Wait for completion } catch (Exception e) { e.printStackTrace(); } // Find the diameter of the tree (longest path) // Step 1: Find the farthest node from any arbitrary node (e.g., node 1) ConcurrentHashMap<Integer, Integer> distances1 = new ConcurrentHashMap<>(); for (int i = 1; i <= n; i++) { distances1.put(i, -1); } distances1.put(1, 0); int farthestNode = parallelBfs(graph, 1, distances1, n); // Step 2: Find the farthest node from the previously found farthest node ConcurrentHashMap<Integer, Integer> distances2 = new ConcurrentHashMap<>(); for (int i = 1; i <= n; i++) { distances2.put(i, -1); } distances2.put(farthestNode, 0); int otherEnd = parallelBfs(graph, farthestNode, distances2, n); // The diameter is the distance between these two nodes int diameter = distances2.get(otherEnd); // For two snow blowers, the optimal solution is to clear all edges // The minimum total distance is 2 * (total length of all sidewalks) - (diameter) int minTotalDistance = 2 * totalLength.get() - diameter; System.out.println(minTotalDistance); } // Parallel BFS to find the farthest node and compute distances private static int parallelBfs(List<List<Edge>> graph, int start, ConcurrentHashMap<Integer, Integer> distance, int n) { ConcurrentLinkedQueue<Integer> queue = new ConcurrentLinkedQueue<>(); queue.add(start); AtomicInteger farthestNode = new AtomicInteger(start); AtomicInteger maxDistance = new AtomicInteger(0); // Process BFS levels in parallel when possible while (!queue.isEmpty()) { // Process current level List<Integer> currentLevel = new ArrayList<>(); Integer node; while ((node = queue.poll()) != null) { currentLevel.add(node); } if (currentLevel.isEmpty()) { break; } // Process nodes in current level in parallel CountDownLatch latch = new CountDownLatch(currentLevel.size()); for (Integer current : currentLevel) { CompletableFuture.runAsync(() -> { try { int currentDistance = distance.get(current); for (Edge edge : graph.get(current)) { if (distance.getOrDefault(edge.to, -1) == -1) { int newDistance = currentDistance + edge.length; distance.put(edge.to, newDistance); queue.add(edge.to); // Update farthest node if needed updateFarthestNode(farthestNode, maxDistance, edge.to, newDistance); } } } finally { latch.countDown(); } }); } try { latch.await(); // Wait for all nodes at this level to be processed } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } return farthestNode.get(); } private static void updateFarthestNode(AtomicInteger farthestNode, AtomicInteger maxDistance, int nodeId, int distance) { boolean updated = false; while (!updated) { int currentMax = maxDistance.get(); if (distance > currentMax) { updated = maxDistance.compareAndSet(currentMax, distance); if (updated) { farthestNode.set(nodeId); } } else { updated = true; // No update needed } } } }

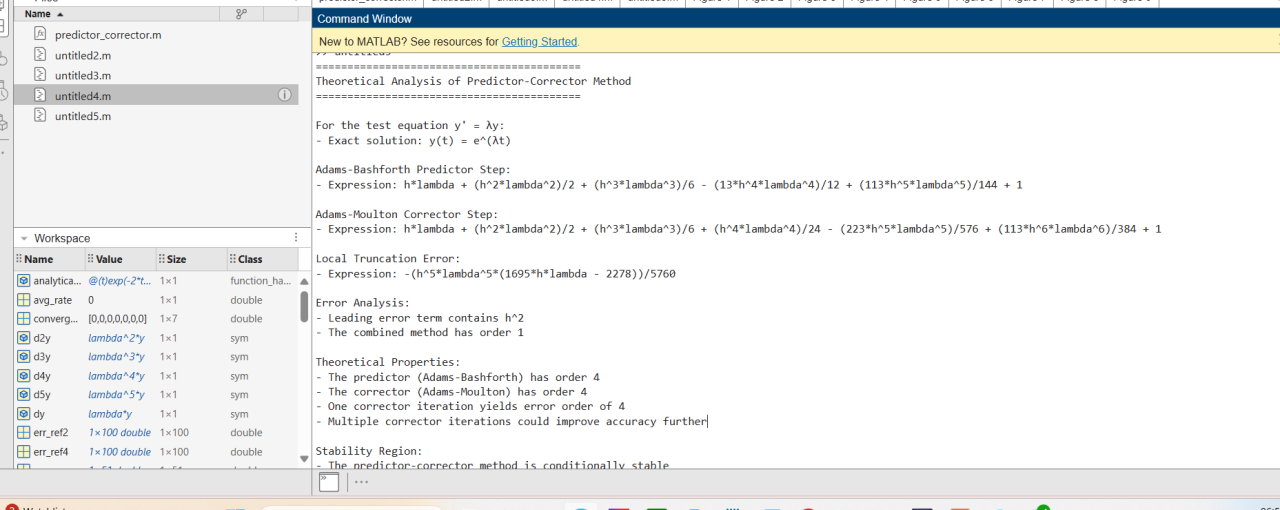
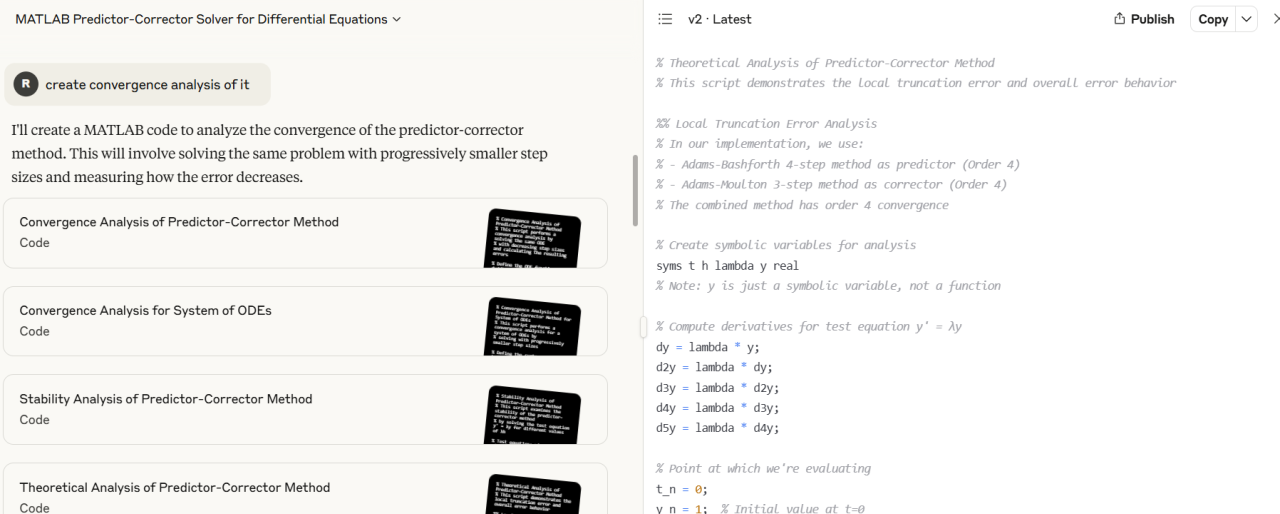
En del av utfordringene med numrisk matematikk er at en ofte må utføre analytisk arbeid, det har vært uungåelig noe analyse av koden - i motsetning av ikke numrisk algoritmisk arbeid. Nå som en kan CLAUDE numriske algoritmer - som ja, også er generert av claude - for å få stabilitets analyse, konvergens analyse, O-notasjon analyse, ...etc så er vist tusen (om ikke milloner) av numeriske algoritmer dummet ned til "kan ikke matematikk" computer scientistens land Hva tenker dere om dette, og er det noen som har erfaring med matematisk analytisk arbeid gjennom claude.ai? Nedenfor vises bilde av claude.ai, og tilhørende utskrift av en diverse analyser, opp mot noen predictor-corrector algoritmer for å løse ODE (numrisk differensial likninger)

AI i edge browser har ny oppsummerings funksjon av video på youtube, kan oppsummere kommentar felt. Jeg tenker at det at en nå kan oppsummere kommentarfelt på youtube er i seg selv en revolusjon, ingen leser dem - men fra nå av kan det faktisk skje Vist nok oppsummerer den ikke innhold i selve videoen, men gjennom eksterne kilder og kommentar felt. Lurer på hva slags opplevelser dere har med denne type funksjonalitet?

Tror det bare blir som det er, noen må validere alt AI gjør - mindre "rutine arbeidere" (utviklere), selvsagt. AI genererer bare, som betyr at noen må verifisere det den gjør og sier - på samme måte som psykriatri validerer mennesker, skole validerer hva folk kan, hvor AI vil kunne lide under de samme validerings problemene som mennesker. For oss, i dag, betyr det i praksis en kontrast økning mellom dem som har utdanning og dem som ikke har utdanning; det er veldig mye enklere nå å generere (det kan lages i fabrikk, kode i software, litteratur, bilder), men det er mye enklere for folk med utdanning å ha noe som kan valideres (sjekke om noe er riktig). På mange måter har hele historien handlet om å redusere kostnaden i å generere, f.eks å genere klær, møbelvarer, elektronikk , biler, på en måte som gjør det lett å validere om dette funker i et reelt miljø; for å redusere risikoen opp mot at noe er feil, så har en brukt simulatorer - konsekvensene av AI er morsomt nok at det blir mye lettere å få lagd disse simulatorene, slik at prisen for å få gjennomført simulering går ned (som igjen må valideres av eksperter, pga problemet til AI). Utviklere har vært "minons" som har generert masse, som så blir validert av "eksperter"; som følge av at at kostnaden for generering går ned, så blir det mer validerings arbeid til "ekspertene" - samme greie som har skjedd i 200 år.

Kjennetegn på chatGPT referanse https://pmc.ncbi.nlm.nih.gov/articles/PMC8385231/?utm_source=chatgpt.com (og for de som ønsker å lese artikkelen, den forklarer hvorfor innvandrere nå må ha A2 språk og ikke bare A1 I ny lov ) For dere som er vant til å jukse, dette er et bra "warning shoot" at referansene er farlig - de får deg til å innrømme juks Det finnes ikke døde referanser lenger, its tagged! R.I.P døde referanser = chatGPT.

Claude.ai kan markere inn fikanter opp mot WCAG 2.1, gitt et vanlig bilde, med tilhørende suksesskriterier Lurer på om noen har erfaring med å teste webdesign på denne måten, vil tro en bruker mer profosjonelle verktøy - men er gratis workaround, som er kinda kul Noen som har erfaring med dette?

En burde på generelt grunnlag ikke bruke AI som referanse uten at innholdet (og referansene til innholdet) er validert av en ekspert (en med relevant utdannelse). En kan potensielt skrive veldig mye gjennom AI, men potensielt kan veldig mye av innholdet være feilaktig - det må valideres.

Burde en bruke https://gamma.app/ AI for effektiv saksforberedelse opp mot møter, saks gjennomgang i møter, og forberedelse opp mot forelesning? I hvilke grad burde en bruke AI til denne type ting? Her er noen punkt om hva det er, og hvorfor det kan brukes. Forberedelse til forelesning Gamma.app kan omgjøre notater, tidligere eksamens oppgaver, samt tekst fra pensum til powerpoint; i tillegg kan en i forkant generere pdf i chatGPT tilsvarende en lecture om ett eller annet tema, tilpasset læringsmål, pensum og tidligere eksamensoppgaver, som kan lastes opp i gamma.app - slik at en deremed får en god powerpoint. Møte forberedelse og saks gjennomgang i møter I utgangspunktet kan gamma.app AI funke som en metodikk for å oppsummere innhold til ulike parter, opp mot et møte - om det måtte være koblet opp mot læringsmiljø, styremøte, foreningsmøte, eller liknende. Forvaltningsloven §17 setter krav til at "så godt opplsyt som mulig før vedtak treffes", noe som må skjønns vurderes opp mot de teknologiske muligheter en har til rådighet. Mer spesifikt står det: "§ 17.(forvaltningsorganets utrednings- og informasjonsplikt). Forvaltningsorganet skal påse at saken er så godt opplyst som mulig før vedtak treffes. Det skal påse at mindreårige parter har fått mulighet til å gi uttrykk for sitt syn, i den grad de er i stand til å danne seg egne synspunkter på det saken gjelder. De mindreåriges syn skal tillegges vekt i samsvar med deres alder og modenhet.[...]" (Lov om behandlingsmåten i forvaltningssaker (forvaltningsloven) - Lovdata) Ved å at en kan gi ulike parter en AI generert oppsummering, i tillegg, så kan dette virke som obligatorisk; videre er det et spørsmål om en burde ta i bruk powerpoint i møter, som er AI-generert, som på en best mulig måte oppsummerer informasjon fra ulike parter - slik at en dermed, i best mulig grad, er"så godt opplsyt som mulig før vedtak treffes".

Argumentene som brukes er ikke lenger reel, dvs argument som "Samtidig sier hun at ingen andre vil kunne overta eller erstatte disse funksjonene på en god måte", som følge av AI og at en nå kan bruke kode generatorer (og kode oversettere) til å kunne vedlikeholde en web-browser på en økonomisk betryggende måte - noe som var vanskelig før, dvs å kode raskt nok til å henge med i svingene (noe som fører en langt inn i historien om Scrum, og "being reactive to change") Tror heller ikke de trenger å selge, i lys av at vi er i AI alderen.

Python Programming Fundamentals Course Examination Course Introduction This examination assesses your understanding of fundamental Python programming concepts covered in the "Python Programming Fundamentals" course. Throughout this course, you have explored: Basic syntax and data structures Control flow (conditionals and loops) Functions and modular programming Object-oriented programming concepts Error handling File operations Basic algorithms and problem-solving techniques This exam will test both your theoretical knowledge and practical coding abilities. For coding questions, you will need to either write complete solutions or fill in missing code sections to complete the given programs. Part I: Python Fundamentals (20 points) 1. Variable Types (5 points) Identify the data type that would be returned by each of the following expressions: a) 5 // 2 b) 7.0 / 2 c) "Hello" + "World" d) [1, 2, 3] + [4, 5] e) {"name": "John", "age": 30}.keys() 2. List Operations (5 points) Complete the missing code to perform the following operations: numbers = [10, 20, 30, 40, 50] # a) Add the value 60 to the end of the list # YOUR CODE HERE # b) Insert the value 15 at index 1 # YOUR CODE HERE # c) Remove the value 30 from the list # YOUR CODE HERE # d) Reverse the list # YOUR CODE HERE # e) Create a new list containing only values greater than 25 result = # YOUR CODE HERE 3. String Manipulation (5 points) Complete the function to convert a string to title case (first letter of each word capitalized) without using the .title() method: def custom_title_case(text): """ Convert a string to title case (capitalize first letter of each word) Args: text (str): Input string to be converted Returns: str: Converted string in title case """ # YOUR CODE HERE # Example usage: # custom_title_case("hello world") should return "Hello World" 4. Dictionary Operations (5 points) Complete the function that takes a list of students with their scores and returns a dictionary with the student names as keys and their grades as values, based on the following grading scale: 90-100: 'A' 80-89: 'B' 70-79: 'C' 60-69: 'D' Below 60: 'F' def assign_grades(students_scores): """ Assign letter grades to students based on their scores Args: students_scores (list): List of tuples containing (student_name, score) Returns: dict: Dictionary with student names as keys and letter grades as values """ # YOUR CODE HERE # Example: # assign_grades([("Alice", 92), ("Bob", 85), ("Charlie", 70), ("David", 55)]) # Should return: {"Alice": "A", "Bob": "B", "Charlie": "C", "David": "F"} Part II: Control Flow (20 points) 5. Conditional Statements (5 points) Complete the following function that determines if a year is a leap year: def is_leap_year(year): """ Determine if a given year is a leap year A leap year is divisible by 4, but not by 100 unless it's also divisible by 400 Args: year (int): Year to check Returns: bool: True if leap year, False otherwise """ # YOUR CODE HERE # Examples: # 2000 and 2020 are leap years # 1900 and 2023 are not leap years 6. Loops (5 points) Complete the function to generate a pattern of asterisks as shown in the example: def generate_pattern(rows): """ Generate a pattern of asterisks Args: rows (int): Number of rows in the pattern Returns: str: The pattern as a string """ # YOUR CODE HERE # Example: # generate_pattern(5) should return: # * # ** # *** # **** # ***** 7. Nested Loops (5 points) Complete the function to create a multiplication table of size n × n: def multiplication_table(n): """ Generate a multiplication table of size n × n Args: n (int): Size of the multiplication table Returns: list: 2D list representing the multiplication table """ # YOUR CODE HERE # Example: # multiplication_table(3) should return: # [[1, 2, 3], [2, 4, 6], [3, 6, 9]] 8. List Comprehensions (5 points) Convert each of the following loop-based code snippets to equivalent list comprehensions: # a) Create a list of squares of numbers from 1 to 10 squares = [] for i in range(1, 11): squares.append(i ** 2) # Convert to list comprehension: squares = # YOUR CODE HERE # b) Filter out odd numbers from a list numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] even_numbers = [] for num in numbers: if num % 2 == 0: even_numbers.append(num) # Convert to list comprehension: even_numbers = # YOUR CODE HERE # c) Create a list of tuples with numbers and their squares numbers = [1, 2, 3, 4, 5] result = [] for num in numbers: result.append((num, num ** 2)) # Convert to list comprehension: result = # YOUR CODE HERE Part III: Functions and Modularity (20 points) 9. Function Parameters (5 points) Complete the function that calculates the total price after applying a discount: def calculate_price(items, discount=0, tax_rate=0.08): """ Calculate the total price after discount and tax Args: items (list): List of item prices discount (float, optional): Discount rate as a decimal (default: 0) tax_rate (float, optional): Tax rate as a decimal (default: 0.08) Returns: float: Final price after discount and tax """ # YOUR CODE HERE # Example: # calculate_price([10, 20, 30], 0.1) should calculate: # Subtotal: 60, After discount: 54, After tax: 58.32 10. Recursive Functions (5 points) Complete the recursive function to calculate the Fibonacci sequence: def fibonacci(n): """ Calculate the nth Fibonacci number recursively Args: n (int): Position in the Fibonacci sequence (0-indexed) Returns: int: The nth Fibonacci number """ # YOUR CODE HERE # Examples: # fibonacci(0) = 0 # fibonacci(1) = 1 # fibonacci(6) = 8 11. Lambda Functions (5 points) Replace the following functions with equivalent lambda expressions: # a) Function to calculate the square of a number def square(x): return x ** 2 # Replace with lambda: square_lambda = # YOUR CODE HERE # b) Function to check if a number is even def is_even(x): return x % 2 == 0 # Replace with lambda: is_even_lambda = # YOUR CODE HERE # c) Function to convert temperature from Celsius to Fahrenheit def celsius_to_fahrenheit(celsius): return (celsius * 9/5) + 32 # Replace with lambda: celsius_to_fahrenheit_lambda = # YOUR CODE HERE 12. Higher-Order Functions (5 points) Complete the following code using map, filter, and reduce (from functools): from functools import reduce numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] # a) Use map to create a list of squares of all numbers squares = # YOUR CODE HERE # b) Use filter to get only the even numbers evens = # YOUR CODE HERE # c) Use reduce to calculate the product of all numbers product = # YOUR CODE HERE # d) Chain operations: get the sum of squares of even numbers result = # YOUR CODE HERE Part IV: Object-Oriented Programming (20 points) 13. Class Definition (5 points) Define a class Rectangle with the following specifications: Attributes: length and width Methods: calculate_area(), calculate_perimeter(), is_square() class Rectangle: """ A class representing a rectangle """ # YOUR CODE HERE # Example usage: # rect = Rectangle(5, 10) # rect.calculate_area() should return 50 # rect.calculate_perimeter() should return 30 # rect.is_square() should return False 14. Inheritance (5 points) Create a class Student that inherits from the following Person class: class Person: def __init__(self, name, age): self.name = name self.age = age def introduce(self): return f"My name is {self.name} and I am {self.age} years old." class Student(Person): """ A class representing a student, inheriting from Person Additional attributes: student_id, courses (list of enrolled courses) Additional methods: enroll(course), display_courses() """ # YOUR CODE HERE # Example usage: # student = Student("Alice", 20, "S12345") # student.introduce() should include student ID # student.enroll("Math 101") # student.display_courses() should show enrolled courses 15. Static and Class Methods (5 points) Complete the BankAccount class with instance, static, and class methods: class BankAccount: interest_rate = 0.02 # Class variable total_accounts = 0 # Class variable to track the number of accounts def __init__(self, account_number, balance=0): self.account_number = account_number self.balance = balance # Increment the total number of accounts BankAccount.total_accounts += 1 def deposit(self, amount): """Instance method to deposit money""" # YOUR CODE HERE def withdraw(self, amount): """Instance method to withdraw money""" # YOUR CODE HERE @classmethod def set_interest_rate(cls, rate): """Class method to set the interest rate for all accounts""" # YOUR CODE HERE @staticmethod def validate_account_number(account_number): """Static method to validate if an account number is valid Valid account numbers must be 10 digits """ # YOUR CODE HERE 16. Magic Methods (5 points) Implement the following magic methods in the Vector class to perform vector operations: class Vector: def __init__(self, x, y, z): self.x = x self.y = y self.z = z def __str__(self): """String representation of the vector""" # YOUR CODE HERE def __add__(self, other): """Add two vectors""" # YOUR CODE HERE def __sub__(self, other): """Subtract other vector from this vector""" # YOUR CODE HERE def __eq__(self, other): """Check if two vectors are equal""" # YOUR CODE HERE def __mul__(self, scalar): """Multiply vector by a scalar""" # YOUR CODE HERE Part V: Error Handling and File Operations (20 points) 17. Exception Handling (5 points) Complete the function to safely divide two numbers, handling potential errors: def safe_divide(a, b): """ Safely divide a by b, handling potential errors Args: a (float): Numerator b (float): Denominator Returns: float: Result of division, or None if error occurs """ # YOUR CODE HERE # Examples: # safe_divide(10, 2) should return 5.0 # safe_divide(10, 0) should handle the ZeroDivisionError # safe_divide("10", 2) should handle the TypeError 18. Custom Exceptions (5 points) Create a custom exception and use it in a function that validates user input: # Define custom exception # YOUR CODE HERE def validate_username(username): """ Validate a username according to the following rules: - Must be between 5 and 20 characters - Must contain only alphanumeric characters and underscores - Must start with a letter Args: username (str): Username to validate Returns: bool: True if valid Raises: InvalidUsernameError: If username is invalid, with appropriate message """ # YOUR CODE HERE 19. File Reading (5 points) Complete the function to read a CSV file and calculate statistics: def analyze_csv(filename): """ Read a CSV file with numeric data and calculate basic statistics The CSV file has headers in the first row and numeric data in all other rows Args: filename (str): Name of the CSV file Returns: dict: Dictionary with column names as keys and dictionaries of statistics as values Each statistics dictionary should have: min, max, mean, sum """ # YOUR CODE HERE # Example CSV format: # Name,Age,Height,Weight # John,28,175,82 # Alice,24,163,55 # ... 20. File Writing (5 points) Complete the function to log message with timestamps to a file: import datetime def log_message(filename, message, mode='a'): """ Log a message with a timestamp to a file Args: filename (str): Name of the log file message (str): Message to log mode (str, optional): File opening mode (default: 'a' for append) """ # YOUR CODE HERE # Example: # log_message("application.log", "User logged in") # Should append a line like: "2023-04-28 14:30:45 - User logged in" Part VI: Problem Solving (20 points) 21. Algorithm Implementation (10 points) Implement a function to find the largest continuous sum in a list: def max_subarray_sum(arr): """ Find the largest sum of any contiguous subarray Args: arr (list): List of integers (positive and negative) Returns: int: Largest sum of any contiguous subarray """ # YOUR CODE HERE # Examples: # max_subarray_sum([-2, 1, -3, 4, -1, 2, 1, -5, 4]) should return 6 (sum of [4, -1, 2, 1]) # max_subarray_sum([-1, -2, -3]) should return -1 (the single largest element) 22. Data Processing (10 points) Complete the function to process a list of transactions and generate a summary: def process_transactions(transactions): """ Process a list of financial transactions and generate a summary Each transaction is a dictionary with keys: - 'date': string in format 'YYYY-MM-DD' - 'amount': float (positive for income, negative for expense) - 'category': string Args: transactions (list): List of transaction dictionaries Returns: dict: Summary with keys: - 'total_income': total positive amounts - 'total_expense': total negative amounts (as positive number) - 'net': income minus expenses - 'categories': dictionary with categories as keys and their total amounts as values - 'monthly': dictionary with months ('YYYY-MM') as keys and their net amounts as values """ # YOUR CODE HERE # Example: # transactions = [ # {'date': '2023-01-15', 'amount': 1000, 'category': 'Salary'}, # {'date': '2023-01-20', 'amount': -50, 'category': 'Food'}, # {'date': '2023-02-10', 'amount': -200, 'category': 'Rent'}, # {'date': '2023-02-15', 'amount': 1000, 'category': 'Salary'}, # ] # should return a dictionary with the appropriate summary Extra Credit: Advanced Python Concepts (10 points) 23. Generators (5 points) Implement a generator function that yields prime numbers: def prime_generator(limit): """ Generator that yields prime numbers up to a given limit Args: limit (int): Upper bound (inclusive) Yields: int: Next prime number """ # YOUR CODE HERE # Example: # list(prime_generator(20)) should return [2, 3, 5, 7, 11, 13, 17, 19] 24. Decorators (5 points) Create a decorator that measures and logs the execution time of functions: import time import functools def timing_decorator(func): """ Decorator that measures and prints the execution time of a function Args: func: The function to decorate Returns: The wrapped function with timing functionality """ # YOUR CODE HERE # Example use: @timing_decorator def slow_function(n): time.sleep(n) return n * n # When calling slow_function(2), it should print the execution time (approximately 2 seconds) End of Examination Total Points: 100 (+10 Extra Credit)

Nedenfor er en eksamen laget i https://claude.ai/, som gir mulighet til å laste ned gjennom pdf fil (som en forsovidt og så kan gjøre i chatGPT), og tilhørende løsnings forslag. Spørsmålet er egentlig litt filosofisk: Burde en gidde å selv stå for arbeidet med å lage repetitive oppgave på en eksamen, og skal en selv bare stå for de oppgaver som er mer kreativ (som forsovidt også kan lages av claude.ai)? AI er ganske skremmende. Min mening er at en burde ha mulighet til å reservere seg mot AI, og da heller få tildelt en vanlig eksamen; videre burde en ha mulighet til å kreve AI-generert eksamen, hvis mange nok mener det er god grunn til dette. Hva tenker dere? Calculus Examination Total Points: 100 Time Allowed: 2 hours Instructions: Show all work for full credit. No calculators permitted unless specified. Part I: Limits and Continuity (20 points) (5 points) Evaluate the following limit: lim(x→3) (x² - 9)/(x - 3) (5 points) Find the value of c that makes the following function continuous on ℝ: f(x) = { x² + 2x if x < 1 cx + 4 if x ≥ 1 } (5 points) Determine if the following limit exists. If it does, find its value: lim(x→0) sin(3x)/x (5 points) Evaluate: lim(x→∞) (1 + 2/x)ˣ Part II: Derivatives (25 points) (5 points) Find the derivative of f(x) = x³ln(x) - 2x²sin(x) (5 points) If f(x) = tan²(3x), find f'(x). (5 points) Find the equation of the tangent line to the curve y = xeˣ at the point (0,0). (5 points) Use implicit differentiation to find dy/dx for the curve: x²y + xy² = 6 (5 points) If f(x) = ∫₀^(x²) cos(t²) dt, find f'(x) using the Fundamental Theorem of Calculus. Part III: Applications of Derivatives (20 points) (5 points) Find the absolute maximum and minimum values of f(x) = x³ - 3x² - 9x + 7 on the interval [-2, 4]. (5 points) A particle moves along a line with position function s(t) = t³ - 6t² + 9t where s is measured in meters and t in seconds. Find: a) The velocity at time t = 2 b) The time(s) when the particle is at rest c) When the particle is moving in the positive direction (5 points) Use Newton's method with the initial approximation x₁ = 2 to find x₂ and x₃ as approximations to the solution of the equation x³ - 2x - 5 = 0. (5 points) Use differentials to approximate the value of √17. Part IV: Integration (20 points) (5 points) Evaluate: ∫ (x² + 1)/x³ dx (5 points) Evaluate: ∫ sin³(x)cos²(x) dx (5 points) Evaluate the definite integral: ∫₀¹ xe^(x²) dx (5 points) Find the area of the region bounded by the curves y = x² and y = 4 - x². Part V: Applications of Integration (15 points) (5 points) Find the volume of the solid obtained by rotating the region bounded by y = x², y = 0, and x = 2 about the x-axis. (5 points) A particle moves along a line with velocity function v(t) = t² - 4t + 3 meters per second. If the particle is at position s = 5 when t = 2, find its position function s(t). (5 points) Find the average value of the function f(x) = sin(x) on the interval [0, π]. Bonus Question: (5 points) Find the general solution to the differential equation: dy/dx = (y² + xy)/(x² + xy) End of Examination Calculus Examination Solution Manual Part I: Limits and Continuity (20 points) 1. Evaluate: lim(x→3) (x² - 9)/(x - 3) Solution: The expression is in indeterminate form 0/0 since direct substitution gives (9-9)/(3-3) = 0/0. We can factor the numerator: (x² - 9)/(x - 3) = ((x - 3)(x + 3))/(x - 3) = x + 3 for x ≠ 3 Therefore: lim(x→3) (x² - 9)/(x - 3) = lim(x→3) (x + 3) = 3 + 3 = 6 2. Find value of c for continuous function: f(x) = { x² + 2x if x < 1 cx + 4 if x ≥ 1 } Solution: For f(x) to be continuous at x = 1, the left and right limits must be equal: lim(x→1⁻) f(x) = lim(x→1⁺) f(x) Left limit: lim(x→1⁻) (x² + 2x) = 1² + 2(1) = 1 + 2 = 3 Right limit: lim(x→1⁺) (cx + 4) = c(1) + 4 = c + 4 For continuity: 3 = c + 4 Therefore: c = -1 3. Determine if limit exists: lim(x→0) sin(3x)/x Solution: Rewrite as: lim(x→0) sin(3x)/x = lim(x→0) [3·sin(3x)/(3x)] We know that lim(u→0) sin(u)/u = 1 Let u = 3x, then as x→0, u→0 lim(x→0) sin(3x)/x = 3·lim(u→0) sin(u)/u = 3·1 = 3 Therefore, the limit exists and equals 3. 4. Evaluate: lim(x→∞) (1 + 2/x)ˣ Solution: This is in the form of the definition of e: lim(x→∞) (1 + 1/x)ˣ = e We can rewrite our limit: lim(x→∞) (1 + 2/x)ˣ = lim(x→∞) [(1 + 2/x)^(x/2)]² = [lim(x→∞) (1 + 2/x)^(x/2)]² Let y = x/2, then as x→∞, y→∞ [lim(y→∞) (1 + 1/(y/2))^y]² = [lim(y→∞) (1 + 2/y)^y]² = e² Therefore: lim(x→∞) (1 + 2/x)ˣ = e² ≈ 7.389 Part II: Derivatives (25 points) 5. Find the derivative of f(x) = x³ln(x) - 2x²sin(x) Solution: Using the product rule and chain rule: For x³ln(x): d/dx[x³ln(x)] = x³·(1/x) + ln(x)·(3x²) = x² + 3x²ln(x) = x²(1 + 3ln(x)) For 2x²sin(x): d/dx[2x²sin(x)] = 2x²·cos(x) + sin(x)·(4x) = 2x²cos(x) + 4xsin(x) Therefore: f'(x) = x²(1 + 3ln(x)) - 2x²cos(x) - 4xsin(x) = x²(1 + 3ln(x) - 2cos(x)) - 4xsin(x) 6. If f(x) = tan²(3x), find f'(x) Solution: Using the chain rule: f'(x) = d/dx[tan²(3x)] = 2tan(3x)·d/dx[tan(3x)] = 2tan(3x)·sec²(3x)·d/dx[3x] = 2tan(3x)·sec²(3x)·3 = 6tan(3x)sec²(3x) Since sec²(θ) = 1 + tan²(θ), we can also write: f'(x) = 6tan(3x)(1 + tan²(3x)) = 6tan(3x) + 6tan³(3x) 7. Find equation of tangent line to y = xeˣ at (0,0) Solution: First, find the derivative: y' = d/dx[xeˣ] = eˣ + x·d/dx[eˣ] = eˣ + xeˣ = eˣ(1 + x) At point (0,0): y'(0) = e⁰(1 + 0) = 1·1 = 1 Using point-slope form of a line: y - y₀ = m(x - x₀) Where (x₀,y₀) = (0,0) and m = 1 The equation of the tangent line is: y - 0 = 1(x - 0) y = x 8. Use implicit differentiation to find dy/dx for x²y + xy² = 6 Solution: Differentiating both sides with respect to x: d/dx[x²y + xy² = 6] For x²y: d/dx[x²y] = 2xy + x²(dy/dx) For xy²: d/dx[xy²] = y² + x·2y(dy/dx) = y² + 2xy(dy/dx) Therefore: 2xy + x²(dy/dx) + y² + 2xy(dy/dx) = 0 x²(dy/dx) + 2xy(dy/dx) = -2xy - y² (dy/dx)(x² + 2xy) = -2xy - y² dy/dx = (-2xy - y²)/(x² + 2xy) dy/dx = -y(2x + y)/(x² + 2xy) 9. If f(x) = ∫₀^(x²) cos(t²) dt, find f'(x) using the Fundamental Theorem of Calculus Solution: By the Fundamental Theorem of Calculus: If F(x) = ∫ₐ^x g(t)dt, then F'(x) = g(x) Here f(x) = ∫₀^(x²) cos(t²) dt, which means: f'(x) = cos((x²)²)·d/dx[x²] = cos(x⁴)·2x Therefore: f'(x) = 2x·cos(x⁴) Part III: Applications of Derivatives (20 points) 10. Find absolute max/min values of f(x) = x³ - 3x² - 9x + 7 on [-2, 4] Solution: Step 1: Find critical points by setting f'(x) = 0 f'(x) = 3x² - 6x - 9 = 3(x² - 2x - 3) = 3(x - 3)(x + 1) f'(x) = 0 when x = 3 or x = -1 Step 2: Evaluate f at critical points and endpoints f(-2) = (-2)³ - 3(-2)² - 9(-2) + 7 = -8 - 12 + 18 + 7 = 5 f(-1) = (-1)³ - 3(-1)² - 9(-1) + 7 = -1 - 3 + 9 + 7 = 12 f(3) = (3)³ - 3(3)² - 9(3) + 7 = 27 - 27 - 27 + 7 = -20 f(4) = (4)³ - 3(4)² - 9(4) + 7 = 64 - 48 - 36 + 7 = -13 Therefore: Absolute maximum: f(-1) = 12 Absolute minimum: f(3) = -20 11. Particle with position s(t) = t³ - 6t² + 9t Solution: a) Velocity at time t = 2: v(t) = s'(t) = 3t² - 12t + 9 v(2) = 3(2)² - 12(2) + 9 = 12 - 24 + 9 = -3 m/s b) Times when particle is at rest: v(t) = 0 3t² - 12t + 9 = 0 3(t² - 4t + 3) = 0 t² - 4t + 3 = 0 Using quadratic formula: t = (4 ± √(16-12))/2 = (4 ± √4)/2 = (4 ± 2)/2 t = 3 or t = 1 c) Particle moves in positive direction when v(t) > 0 3t² - 12t + 9 > 0 For t < 1 or t > 3, the velocity is positive Therefore, the particle moves in the positive direction when t ∈ (-∞, 1) ∪ (3, ∞) 12. Newton's method for x³ - 2x - 5 = 0 with x₁ = 2 Solution: For Newton's method, we use the formula: xₙ₊₁ = xₙ - f(xₙ)/f'(xₙ) f(x) = x³ - 2x - 5 f'(x) = 3x² - 2 For x₁ = 2: f(2) = 2³ - 2(2) - 5 = 8 - 4 - 5 = -1 f'(2) = 3(2)² - 2 = 12 - 2 = 10 x₂ = 2 - (-1/10) = 2 + 0.1 = 2.1 For x₂ = 2.1: f(2.1) = (2.1)³ - 2(2.1) - 5 = 9.261 - 4.2 - 5 = 0.061 f'(2.1) = 3(2.1)² - 2 = 3(4.41) - 2 = 13.23 - 2 = 11.23 x₃ = 2.1 - (0.061/11.23) = 2.1 - 0.005433 ≈ 2.095 Therefore: x₂ = 2.1 and x₃ ≈ 2.095 13. Use differentials to approximate √17 Solution: We can use the formula: f(a + h) ≈ f(a) + f'(a)·h Let f(x) = √x, a = 16, and h = 1 (since 17 = 16 + 1) f'(x) = 1/(2√x) f(16) = √16 = 4 f'(16) = 1/(2√16) = 1/(2·4) = 1/8 Therefore: √17 ≈ √16 + (1/8)·1 = 4 + 0.125 = 4.125 Part IV: Integration (20 points) 14. Evaluate: ∫ (x² + 1)/x³ dx Solution: ∫ (x² + 1)/x³ dx = ∫ (x²/x³ + 1/x³) dx = ∫ (1/x + 1/x³) dx = ∫ x⁻¹ dx + ∫ x⁻³ dx = ln|x| + (-1/2)x⁻² + C = ln|x| - 1/(2x²) + C 15. Evaluate: ∫ sin³(x)cos²(x) dx Solution: Let u = sin(x), then du = cos(x) dx This gives: cos(x) dx = du ∫ sin³(x)cos²(x) dx = ∫ u³cos(x)cos(x) dx = ∫ u³ cos²(x) dx We know sin²(x) + cos²(x) = 1, so cos²(x) = 1 - sin²(x) = 1 - u² Therefore: ∫ u³(1 - u²) du = ∫ (u³ - u⁵) du = u⁴/4 - u⁶/6 + C = sin⁴(x)/4 - sin⁶(x)/6 + C 16. Evaluate: ∫₀¹ xe^(x²) dx Solution: Let u = x², then du = 2x dx, or x dx = du/2 ∫₀¹ xe^(x²) dx = ∫₀¹ (1/2)e^(x²)(2x dx) = (1/2)∫₀¹ e^u du When x = 0, u = 0; when x = 1, u = 1 (1/2)∫₀¹ e^u du = (1/2)[e^u]₀¹ = (1/2)(e¹ - e⁰) = (1/2)(e - 1) = (e - 1)/2 17. Find area between y = x² and y = 4 - x² Solution: First, find intersection points by setting the equations equal: x² = 4 - x² 2x² = 4 x² = 2 x = ±√2 The area is: ∫₍₋√2₎^√2 [(4 - x²) - x²] dx = ∫₍₋√2₎^√2 [4 - 2x²] dx = [4x - (2x³/3)]₍₋√2₎^√2 = [4√2 - (2(√2)³/3)] - [4(-√2) - (2(-√2)³/3)] = [4√2 - (2·2√2/3)] - [-4√2 - (-2·2√2/3)] = [4√2 - (4√2/3)] - [-4√2 + (4√2/3)] = [4√2(1 - 1/3)] - [-4√2(1 - 1/3)] = [(8√2/3)] - [-(8√2/3)] = 16√2/3 ≈ 7.54 square units Part V: Applications of Integration (15 points) 18. Volume from rotating y = x², y = 0, x = 2 around x-axis Solution: Using the disk method, the volume is: V = π∫ₐ^b [f(x)]² dx For rotation around the x-axis from x = 0 to x = 2: V = π∫₀^2 (x²)² dx = π∫₀^2 x⁴ dx = π[x⁵/5]₀^2 = π(2⁵/5 - 0) = π(32/5) = 32π/5 ≈ 20.11 cubic units 19. Particle with v(t) = t² - 4t + 3, s(2) = 5 Solution: To find position function, integrate the velocity: s(t) = ∫ v(t) dt = ∫(t² - 4t + 3) dt = t³/3 - 2t² + 3t + C Given s(2) = 5: 5 = (2³/3) - 2(2)² + 3(2) + C 5 = 8/3 - 8 + 6 + C 5 = 8/3 - 2 + C C = 5 - 8/3 + 2 = 7 - 8/3 = (21-8)/3 = 13/3 Therefore: s(t) = t³/3 - 2t² + 3t + 13/3 20. Average value of f(x) = sin(x) on [0, π] Solution: The average value is given by: f_avg = (1/(b-a))∫ₐ^b f(x) dx For f(x) = sin(x) on [0, π]: f_avg = (1/π)∫₀^π sin(x) dx = (1/π)[-cos(x)]₀^π = (1/π)[-cos(π) - (-cos(0))] = (1/π)[-(−1) - (-1)] = (1/π)[1 + 1] = 2/π ≈ 0.637 Bonus Question (5 points) Find the general solution to: dy/dx = (y² + xy)/(x² + xy) Solution: This is a homogeneous differential equation. Let y = vx where v is a function of x. Then dy/dx = v + x(dv/dx) Substituting: v + x(dv/dx) = (v²x² + vx²)/(x² + vx²) v + x(dv/dx) = (v²x + vx)/(x + vx) v + x(dv/dx) = v(vx + x)/(x + vx) = v Therefore: x(dv/dx) = 0, which means dv/dx = 0 This implies v is constant: v = C where C is any constant Since y = vx, the general solution is: y = Cx Where C is an arbitrary constant of integration.