1.1 Elementære sifreringer Lagt til 22-05-07Kryptografi er designet og bruken av kommunikasjons skjemaer, tilsiktet å gjemme beskjeden i en melding for alle andre enn påtenkt mottaker.Kryptoanalyse er tiltaket for å forhindre lete i systemer; knekke koden.Studier av kryptografi og kryptoanalyse kalles kryptologi og er fokusen på dette kapittelet. Senere vil jeg beskrive noen nokså sofistikerte kryptografiske systemer, men jeg begynner med noen få elementære eksempler.1.1.1 Substitusjonelle sifreringer Lagt til 22-05-07Substitusjonelle sifreringer er den hverdagslige sorten av kryptering som man kan finne i avisen under kryssord- og oppgave-avdelingen, der hver bokstav i alfabetet er byttet med nummer. (LES: Kodekryss). I versjonen Julius Cæsar utviklet, er hver bokstav i alfabetet byttet med bokstaven 3 plasser frem. F.eks om en bokstav i det orginale brevet, eller i klartekst er "A", vil tilhørende bokstav i den krypterte beskjeden være "D", osv som vist her:

Klartekst: A B C ... X Y ZKryptert: D E F ... A B C

Vi kan uttrykke denne sifreringen matematisk ved å tilegne hvert nummer til en bokstav:

A -> 0, B -> 1, ..., Z -> 25.

Om "x" representerer en bokstav i klartekst og "y" den tilhørende verdien i den krypterte teksten, vil Julius Cæsar sin krypteringsmetode bli uttrykt slik:

y = x + 3 (mod 26)

Der "(mod 26)" betyr at du tar resten du får ved å dividere med 26. (Mye mer om modulær regning senere i dette kapittelet.)Om du tilhenger eller en ekspert på å knekke kodekryss i søndagsavisen, vil du finne det overraskende at Cæsar klarte å holde beskjeder hemmelig med denne simple strategien.En enkel generalisering av Cæsar-sifferingen er uttrykt med ligningen:

 y = ax + b (mod 26)

Der a og b er heltall.Et spesielt tilfelle er ROT13, der A = 1 og B = 13. Dette brukes av mange ute på nettet til å gjemme meldinger og fungerer på samme måte som Cæsar, bare at hver bokstav i alfabetet blir flyttet 13 plasser frem.Det er interessant å spørre om noen verdier av A og B er bedre enn andre. En videre generalisering er å bruke en vilkårlig ombytting av alfabetet.Hvordan går du frem for å knekke mønsteret til en kryptering? Teknikken som brukes standard er meget kjent i dag, men var ikke det på den romerske tiden. Denne kalles: "Hyppighets analyse". La oss anta at personen som skal finne ut av dette, vet hva slags språk beskjeden er skrevet i; La oss si det er Engelsk. I en typisk Engelsk tekst, vises hver bokstav med en viss hyppighet. Den mest kjente bokstaven i det Engelske alfabetet er E; om du vilkårlig trykker på skjermen et sted når du har et dokument på skjermen full av tekst, vil du i ca 12,7% av tilfellene treffe bokstaven E.Her er en tabell som gir hyppigheten til alle bokstavene, som er regnet ut av en tekst sammensatt av diverse noveller og artikler fra aviser og slikt på over 300,000 bokstaver.Tabell over hyppighet:

Vi kan bruke denne tabellen til å knekke den substitusjonelle sifreringen som følger:Om vi har den krypterte beskjeden, kan vi telle hvor mange ganger hver bokstav blir vist. Om meldingen er lang nok, vil hyppigheten på hvor ofte tallene blir vist hjelpe oss med å gjette hvordan hvert tegn skal bli dekryptert.F.eks om "V" forekommer ca 13% av gangene, gjetter vi på at "V" representerer bokstaven "E". Med en gang vi har gjettet korrekt på et par av bokstavene, kan vi se etter kjente ord og slikt. En relatert teknikk er å lete etter dobbeltkonsonanter som ofte forekommer sammen.1.1.2 Vigenère Sifrering Lagt til 23-05-07Vi vurderer nå en ny sifrering som er mer sofistikert enn enkel substitusjon.Det ble oppfunnet av Giovan Batista Belaso på 1600-tallet og senere ukorrekt tilskrevet til Blaise de Vigenère og gitt hans navn. (Vigenère tenkte ut en mer kraftfull variasjon til hans sifrering, der meldingen i seg selv ble brukt for å lage nøkkelen.) Den hemmelige nøkkelen i dette eksempelet er en nøkkel, eller en frase. Den enkleste måten å forklare sifreringen er ved å gi et eksempel; i følgende beskjed er "Meet me at midnight" (Bruker denne fordi den er "kjent") og nøkkelen er "quantum" (Ikke en nøkkel Belaso eller Vigenère ville ha brukt)

Klartekst:   M   E   E   T   M   E   A   T   M   I   D   N   I   G  H   TNøkkel:   Q   U   A   N   T   U   M   Q   U   A   N   T   U   M  Q   UKryptert:   C   Y   E   G   F   Y   M   J   G   I   Q   G   C   S  X   N

For å generere denne sifreringsteksten, har jeg assosiert et heltall for hver bokstav, som vist tidligere.

A -> 0, B -> 1, etc.;

I hver kolonne over har jeg lagt til: "mod 26", nummerene som korresponderer med angitt bokstav i klartekst og nøkkelen. F.eks, den første bokstaven i sifreringen er som følger:

M + Q -> 12+16 (mod 26) = 2 -> C

Med andre ord, hver bokstav som er kryptert med sifreringen til Cæsar - krypteringen er en syklisk skifting av alfabetet - men forskjellige bokstaver kan bli byttet med forskjellig sum.I eksempelet over er 6 forskjellige Cæsar sifreringer brukt i et mønster som repeterer 7 bokstaver. Mottakeren av beskjeden vet nøkkelen og kan enkelt lese klarteksten ved å trekke fra tilhørende bokstav i nøkkelen fra hver enkelt bokstav.Legg merke til hvordan denne sifreringen forbedrer seg på det enkle substitusjons skjemaet. Bokstaven M oppstår 3 ganger i klarteksten og har blitt kryptert forskjellig hver gang. Gjensidig så vises G 3 ganger i den krypterte teksten og hver gang står den for forskjellige bokstaver i klarteksten. Men en enkel analyse av hyppigheten vil aldri bli i nærheten av så effektiv som den er mot en substitusjonell kryptering.Uansett, du kan fortsatt bruke hyppigheten til å løse sifreringen om meldingen er lang nok. La oss tenke oss at den som skal løse meldingen finner ut lengden på nøkkelen som blir repetert. La oss si at lengden er 7 som i eksempelet over. Da ville hver syvende bokstav vært kryptert med samme Cæsar sifreringen, som kan bli løst ved å gjøre analyse av hyppigheten på kun de 7 første bokstavene i den krypterte meldingen. Så problemet er ikke stort så fort vi får vite lengden på nøkkelen.Men hvordan kan personen som skal løse beskjeden finne ut lengden på nøkkelen?En metode er å lete etter repeterte rekkene av bokstaver. F.eks, i en lang beskjed er sannsynligheten stor for at ordet "the vil bli kryptert på samme måte flere ganger og vil derfor produsere de samme 3 bokstavene i en sekvens flere ganger. Så om analytikeren (personen som skal løse det) ser f.eks, 3 eksempler på "rqv", vil det andre eksempelet forflytte seg fra det første med 21 steg, og tredje fra andre med 56 steg, han eller hun kunne rimelig lett gjette at den repeterte nøkkelen var på 7 bokstaver. Siden 7 er det eneste positive heltallet (sett bort fra 1) som kan deles på både 21 og 56.Selvfølgelig ville å gjette noe slikt bli mer sikkert om flere repetisjoner ble oppdaget, siden det alltid er mulighet for at en rekke bokstaver i den krypterte teksten blir repetert ved ren tilfeldighet. Denne metoden for å knekke Vigenère sifreringen ble oppdaget på 1900-tallet av Friedrich Kasiski.En alternativ versjon av Vigenère sifreringen bytter om den repeterte nøkkelen med en "løpende nøkkel". Som regel en lett tilgjengelig tekst som er minst like lang som beskjeden. F.eks, kan vi bruke den Amerikanske grunnloven som nøkkel. Vi starter med introduksjonen, og da vil beskjeden: "Meet me at midnight" se ut som dette:

Klartekst:   M   E   E   T   M   E   A   T   M   I   D   N   I   G  H   TNøkkel:   W   E   T   H   E   P   E   O   P   L   E   O   F   T  H   EKryptert:   I   I   X   A   Q   T   E   H   B   T   H   B   N   Z  O   X

Mottakeren av beskjeden; vitende om nøkkelen, kan nå enkelt igjen løse det. Bokstav for bokstav fra den krypterte teksten for å få opp den orginale beskjeden.Under er et bilde som kan vise litt hvordan tabellen fungerer.Det viser hvordan bokstaven J blir kryptert med nøkkelen E for å produsere N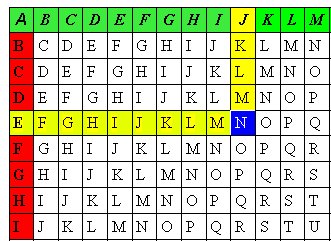Hele tabellen finner du her:

1.1.3 Engangsblokk Lagt til 25-05-07Det som gjør Vigenère sifreringen usikker, selv med en løpende nøkkel som vist over, er at nøkkelen alltid har en struktur som kan bli oppdaget av analytiker.Nøkkelen har en bit av en Engelsk tekst, og engelsk har definitivt en struktur.Den naturlige veien for å unnslippe dette problemet er å bruke en løpende nøkkel som består av tilfeldige bokstaver.Nøkkelen jeg viser under, er laget ved rett og slett skrive opp alfabetet; lukke øynene og peke et sted på arket.

Klartekst:   M   E   E   T   M   E   A   T   M   I   D   N   I   G  H   TNøkkel:   P   O   V   N   H   U   J   B   K   R   C   J   D   C  O   FKryptert:   B   S   Z   G   T   Y   J   U   W   Z   F   W   L   I  V   Y

Selvfølgelig på mottakeren av beskjeden også ha nøkkelen.I dette eksempelet, selv om det er nok av struktur i klarteksten.Er tilfeldigheten i nøkkelen - om den virkelig er tilfeldig - en garanti for at den krypterte teksten vil være helt uten struktur. Dette kryptografiske skjemaet kan derfor ikke bli knekt med kryptoanalyse. (En sniklytter kunne prøvd andre angrep som å avbryte at beskjeden kommer frem til mottakeren.) Vi antar her at nøkkelen er minst like lang som beskjeden, slik at den ikke trenger å bli repetert.Det kan og legges til, at for total sikkerhet er det viktig at nøkkelen kun blir brukt én gang. Om den blir brukt 2 ganger, kan en sniklytter lett sammenligne 2 krypterte tekster og se etter mønster. Denne metoden for kryptering - en tilfeldig nøkkel som kun blir brukt 1 gang - kalles "Engangsblokk" (One-time pad).Foreslått at nøkkelen blir kopiert til et papir; levert til mottaker; brukt 1 gang og ødelagt etterpå.Nå for tiden er det mye mer informasjon som blir formidlet fra sted til sted i sin digitale form, og kan bli lest av datamaskiner som en sekvens av 0 og 1. En engangsblokk fungerer fint for et slikt program, nøkkelen i dette tilfellet - en tilfeldig binær rekke. F.eks, kan du se følgende beskjed, og tenke at den er ganske så uintressant. (Denne gangen ble en mynt brukt, for å bestemme 0 (krone) eller 1 (mynt).

Klartekst:   0   1   0   1   0   1   0   1   0   1   0   1   0   1   0   1Nøkkel:   1   0   0   1   0   0   1   0   0   1   0   0   0   0   1   1Kryptert:   1   1   0   0   0   1   1   1   0   0   0   1   0   1   1   0

1.2 Gåte (Enigma) Lagt til 31-05-07Gjennom min artikkel så langt om kryptografi, har jeg prøvd å ikke være altfor detaljert. Men det er et historisk eksempel jeg ikke kan hoppe over, nemlig; Enigma sifreringen, brukt av det Tyske militæret i andre verdenskrig.Enigma betyr Gåte.Enigma sifreringen er mer kompleks enn sifreringene jeg har gått igjennom så langt. Selv om den kan bli beskrevet i bare matematiske termer og i prinsippet bli implementert med hendene, er sifreringen dypt knyttet til et mekanisk apparat; Enigma-maskinen. I denne seksjonen vil jeg beskrive en litt forenklet versjon av Enigma-maskinen og sifreringen den genererer.1.2.1 Enigma-sifreringen (Gåte-sifreringen) Lagt til 31-05-07Tips: Jeg kommer til å bruke ordet "orientering" mye, det kan også bety plassering i mange tilfeller.Hovedkomponentene i den kryptografiske maskinen er:

1. Støpsel-brettet
2. Rotorene
3. Reflektoren / Speilet

Hver av disse delene har en effekt for å omstille alfabetet, og i hvert tilfelle er omstillingen utrettet av elektroniske ledninger / metalltråder, som vi kan forestille oss kobler inndata bokstaven med utdata bokstaven. Den totale av alle delene oppnår du ved å følge alle kablene rundt i maskinen. Fra den orginale inndata bokstaven; skrevet på et tastatur, til utdata bokstaven som er indikert av blinkingen på en lyspære med den tilhørende bokstaven.Jeg vil nå prøve å beskrive hvert komponent mer nøye.1) Støpsel-brettet inkluderer en rekke av 26 "plugger", 1 for hver bokstav i det engelske alfabetet, 6 elektriske kabler, hver av disse kan bli koblet inn i 2 av "pluggene" for å bytte om på disse 2 bokstavene. (Hver "plugg" består av 2 hull; 1 inndata og 1 utdata. Hver elektriske kabel består av 2 kabler - Noen sender bokstaven B til bokstaven J til eksempel. Vil den andre kabelen sende J til B). Alle bokstavene som ikke er en del av utvekslingen forholder seg uforandret. La oss kalle Støpsel-brettets ombytting for A; - Det er en funksjon som kartlegger / planlegger alfabetet til seg selv. Om x er en inndata-bokstav, kan vi da skrive Ax (uten parantes) for å indikere støpsel-brettets utdata. Legg merke til den omvendte funksjonen A^−1 ("^" = opphøyd i), som tar en gitt utdata fra støpsel-brettet til den tilhørende inndata, som er det samme som A. Dette er viktige fakta i det som følger.2) Hver rotor er en disk med 26 inndata lokasjoner organisert i en sirkel på den ene siden, og 26 utdata lokasjoner organisert i en identisk sirkel på den andre siden. På innsiden av en rotor, er det en ledning som strekker seg fra hver av inndata lokasjonene til hver av utdata lokasjonene, og tilsammen gjennomfører de 26 ledningene en komplisert omflytting uten noen spesiell symmetri. Utdataen til støpsel-brettet ble inndataen til den første rotoren, utdataen til den første roteren ble inndata til den andre rotoren, osv. I den orginale Enigma-maskinen brukt av det tyske militæret, var det 3 standard rotorer, hver av dem legemliggjorde en forskjellig ombytting.3) Reflektoren / Speilet gjør sine handlinger basert på utdataen til den siste rotoren og påvirker en ombytting, som det med støpsel-brettet. Simpelten utveksler bokstaver i par. Ulikt utvekslingen til støpsel-brettet er utvekslingen til reflektoren / speilet fastsatt og kan ikke bli endret av operatøren til maskinen. (I det minste ikke i den enkle versjonen av Enigma som jeg skriver om her. (Det var andre versjoner som tillot litt frihet for å stille reflektoren / speilet.)) - Jeg må ikke glemme å nevne at ombyttingen ikke er begrenset til kun 6 bokstaver; hver bokstav blir sendt til en ny bokstav. Jeg vil kalle refelektorens ombytting for B, og vi noterer at B^-1 = B ("^" = opphøyd i (som nevnt tidligere))La oss nå følge veien der en inndata-bokstav leder til en særskilt utdata-bokstav. Som jeg har underforstått over, vil inndata-bokstavens første sammenstøt være med ombyttingen til støpsel-brettet. Deretter hver rotors ombytting i rekke og rad, før den støter på ombyttingen til reflektoren / speilet. Etter det, går veien bakover gjennom rotorene (i reversert rekkefølge) og til slutt gjennom støpsel-brettet igjen, før den kommer med utdata som blir indikert av merkede lyspærer. Hele veien er vist som et skjema av et forenklet alfabet i Fig. 1.1 - Legg merke til at fordi reflektoren ikke etterlater noen bokstav uendret, vil ikke Enigma-maskinen gjøre det heller i sin helhet; den koder aldri en singel bokstav for seg selv.Figur. 1.1: Skjematisk illustrasjon av de kryptografiske hovedkomponentene i Enigma-maskinen med et alfabet på 4 bokstaver. Her er bokstaven A kryptert som bokstaven C. (De spesifikke kantene og vinklene innen rotoren har ingen spesiell betydning. Alt som betyr noe i hver rotor er at kartleggingen / planleggingen går mellom venstresiden og høyresiden.)Det mest karakteristiske og subtile kjennetegnet ved Enigma-maskinen er dette: Selvom hver rotor har en fastsatt ombytting kablet til den, er orienteringen med respekt for de andre rotorene og med aktelse for de andre komponentene den som kan skifte fra ett tastetrykk til et annet. Det er en orientering i hver rotor som vi kaller "standard" orientering. La R(1) være ombyttingen utført av den første(1) rotoren når den ved sin standard orientering. Så, om rotorens orientering blir rotert fra sin standard orientering med ett "steg", altså med 1/26 av en full omdreining. Blir det som at ombyttingen R(1) anvendes til et alfabet som hadde blitt flyttet med 1 bokstav. I sin virkning; gjennomfører nå rotoren ombyttingen:

S^-1 R(1) S,

Der S er den simple ombyttingen:

A -> B -> ... -> Z -> A

og S^-1 som det motsatte. (Her er rekkefølgen av funksjonen fra høyre til venstre, så fremover-skiftet blir anvendt først.) Effekten av en en-stegs rotasjon er illustrert i Fig. 1.2 Om rotoren har blitt rotert med n steg fra standard orienteringen (i samme retningen som før), ombyttingen den gjennomfører er: Hvor S^-n = (S^-1)^n; som er, S^-n motsetningen til S anvendt n ganger.Figur 1.2: Er den samme som Fig. 1.1 med unntak av at den første rotoren (Den til venstre) har avansert med 1 steg. Nå er bokstaven A kryptert som bokstaven D. De ledningene som ser ut til å forsvinne ut fra toppen av den første rotoren, fortsetter på bunnen.På et hvilket som helst gitt tastetrykk, har hver rotor en spesifikk orientering som er uttrykt i verdien til n i likningen (1.1). Om det er tre rotorer, er det 3 slike instanser: n(1); n(2); n(3) som hver tar verdier fra 0 til 25, n(2) er avansert med 1 enhet. (Dette er hva som er spesielt med "standard" orientering mtp den første rotoren.) Liknende, n(3) er avansert med 1 enhet bare når n(2) skifter fra 25 til 0. (Du kan tenke deg at når 0 går til 9, blir det 10 (1 og 0), det samme gjelder med 99 til 100 (1 + 0 og siste blir 0) osv.) Selvom antall tastetrykk er krevd før alle rotorene returnerer til sin orginale orientering som er 26^3 = 17567.La oss putte alle disse delene sammen, og skrive ned kartleggingen / planleggingen som maskinen implementerer i et gitt tastetrykk (igjen, dette uttrykket skal leses fra høyre til venstre):Erindre at A og B er ombyttinger påvirket av støpsel-brettet og reflektoren / speilet henholdsvis. Vi kan forenkle dette uttrykket litt ved å skrive ut motsetningene til produktene. Du kan også verifisere at om C og D er motsettende funksjoner definert av samme sett. Det motsettende produktet til CD er produktet av motsetningen i den reverserte rekkefølgen. Dvs:

([i]CD[/i])^1 = D^-1 C^-1[code](PS: Noter at D^-1 C^-1 CD er identifikasjonsfunksjonen)Altså kan vi skrive:Bruke denne faktaen, og kombinere faktorene når det er mulig.Planleggingen i [color=green]likningen (1.2)[/color] kan bli omskrevet som:I den virkelige Enigma-maskinen er [i]rekkefølgen[/i] av disse 3 rotorene mulig å endre; dvs, hver rotor kan bli tatt ut, og satt på en annen plass. Selv om rekkefølgen på ombyttingene R(1), R(2) og R(3) reagerer, ikke trenger å være den samme som i [color=green]likningen (1.3)[/color]. ..senere vil jeg muligens skrive om modulær regning, hill sifreringen, DES, AES, RSA og PKE..                               Sist oppdatert (05-06-07)